ミロのビーナスからアップルまで…「黄金比」はなぜ美しい？

アップルマークもツイッターの鳥も「フィボナッチ数列」？

次の数列はあるルールに従っています。

1、1、2、3、5、8、13、21、34…

34の次の数字がわかるでしょうか？

実はこの数列は、直前の２つの数を足し合わせて次の数を作るという規則なっています。21＋34＝55ですから、34の次は55です。このような数列のことをフィボナッチ数列といいます。

フィボナッチは13世紀にイタリアで活躍した数学者です。フィボナッチは『算番（さんばん）の書』という著作の中で、一組のつがいの子ウサギが1ヶ月後に大人になり、その後は毎月1つがいずつ子ウサギを出産したとすると、つがいの組数は1年間で何組になるかという問題を解決して見せました（下の図参照）。そのときに登場したのがフィボナッチ数列です。

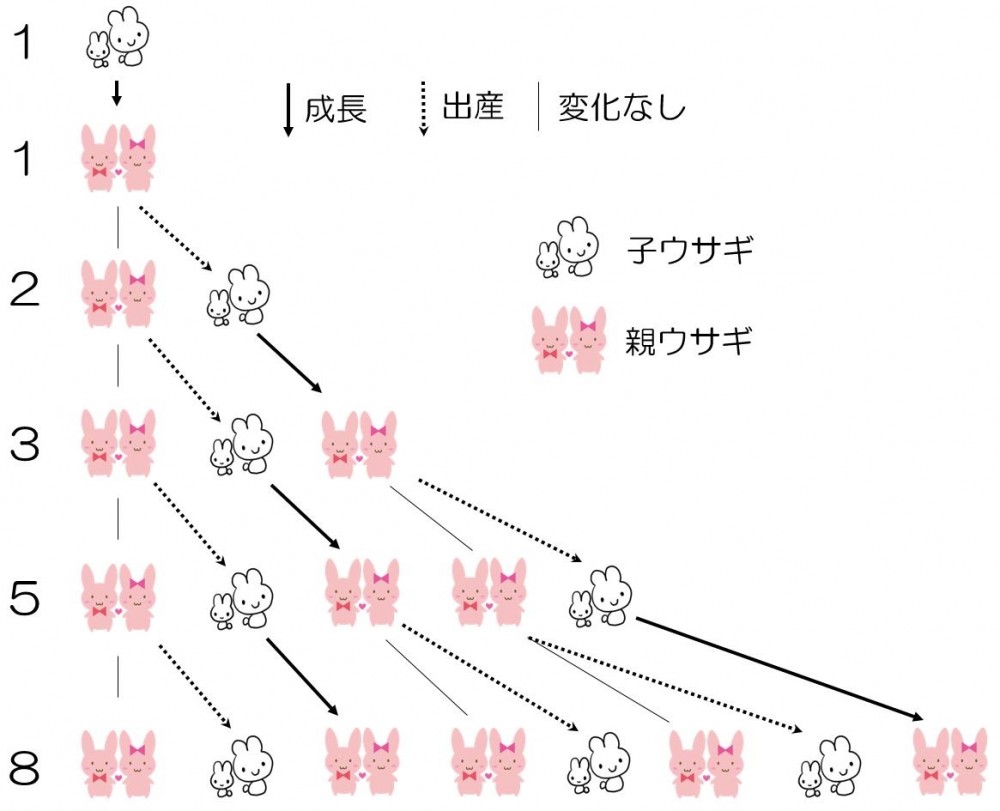
実は、このフィボナッチ数列は黄金比と深い関係があります。

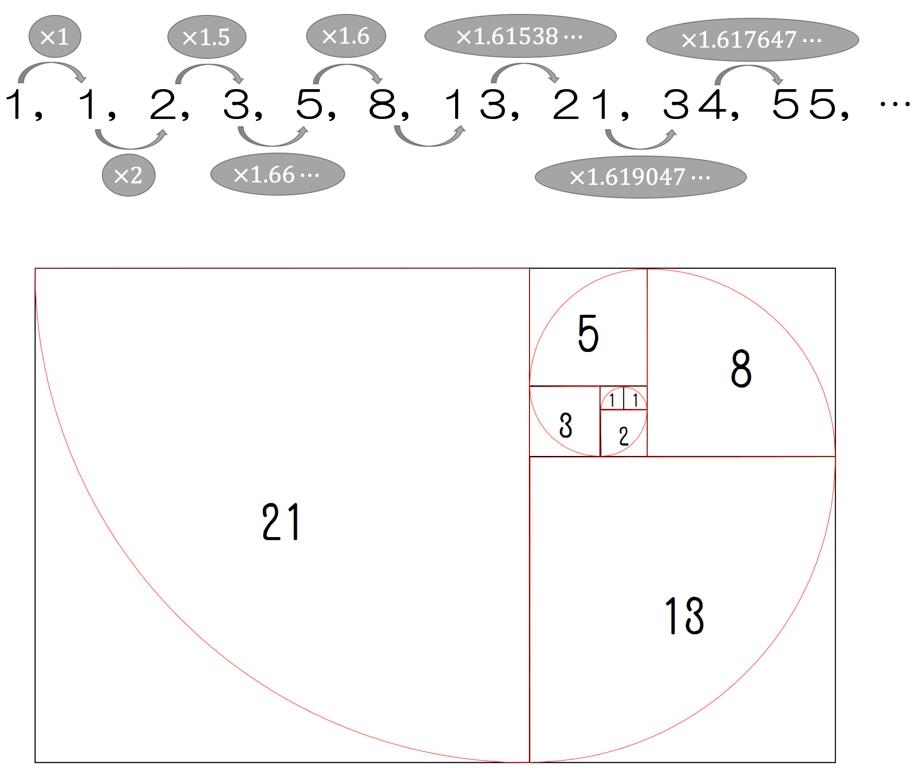
フィボナッチ数列の、となりあう数の比は数が大きくなればなるほど黄金比（1.618…）に近づくのです。

そのため、フィボナッチ数列を一辺の長さとする正方形を並べていくと、先ほどご紹介した黄金長方形とよく似た形となり、その角を滑らかに繋いだ曲線も対数螺旋の一種です。

また、アップルのりんごマークやツイッターの鳥のマークをはじめ、非常に多くのロゴデザインがフィボナッチ数列に登場する数を半径に持つ円を使ってデザインされています。フィボナッチ数列が黄金比に通じることから、関連する円を使ったデザインもまた、美しく感じるからでしょう。

（出典：『東大→JAXA→人気数学塾塾長が書いた数に強くなる本』）